Kenneth Arrow (1921-2017) bio je američki ekonomista koji je 1972. čak dobio i Nobelovu nagradu za ekonomiju. Međutim, iako je bio matematičar i ekonomista dao je zanimljiv doprinos promišljanjima demokratije kroz nešto što se zove Arrowljeva opća teorema nemogućnosti.
Ova teorema iz 1951. godine bila je sastavni dio njegove doktorske disertacije koja se bavila teorijama nemogućnosti koje su u to vrijeme bile popularno igralište za matematičare. Međutim, Arrow je sa svojim radom izišao iz okvira matematike, te snažno utjecao na društvene nauke.
Naime, opća teorema nemogućnosti Kennetha Arrowa je u suštini matematički dokaz da savršen izborni sistem ne postoji i da je jednostavno matematički nemoguće da se racionalnim kolektivnim biranjem ispoštuju temeljna demokratska načela. Svaki izborni sistem je prema ovoj teoremi ili nepošten ili nerazuman.
Ovo je natjeralo brojne mislioce na propitivanje načina na koji funkcionišu demokratski sistemi, a dovelo je i do razvoja nečega što se zove teorija društvenog izbora. Pogledajmo o čemu se tu radi…
Kad su u pitanju individualni izbori, stvar je poprilično jasna. Naprimjer, neko voli gazirani sok više od limunade, a limunadu više od obične vode. U ovom je kontekstu lako govoriti o individualnom izboru i jednostavnom logikom zaključiti kako će osoba vođena isključivo vlastitim preferencama u kafiću prije naručiti gazirani sok nego običnu vodu.

Međutim, kolektivno biranje predstavlja skupljanje pojedinačnih preferenci kako bi se došlo do neke zajedničke preference i da bi se kao grupa došlo do odabira poput ovog između soka, limunade i vode. Postoji nekoliko načina kako se dolazi do ovog izbora.
Jedan od njih je većinski izborni sistem gdje se izabranim smatra onaj koji je osvojio najviše glasova – odnosno relativnu ili kvalificiranu (apsolutnu) većinu. Tako se, naprimjer, u našoj zemlji biraju načelnici općina – pobjednik je jednostavno onaj kandidat sa najvećim procentom glasova. Drugi sistem koji nam je blizak je sistem u kojem dva kandidata sa najvećim brojem glasova idu u drugi krug izbora ukoliko niko nije osvojio natpolovičnu većinu u prvom krugu. Tako se, naprimjer, bira predsjednik Hrvatske.
Postoje i pluralni i preferencijalni sistemi, zatim i sistemi u kojima glasovi nemaju jednaku težinu, ali Arrowljeva teorema ima zamjerke koje se odnose na sve njih. Generalno, te zamjerke kažu kako nije moguće u isto vrijeme ispoštovati svačiji redoslijed preferenci i ostati u okvirima izbornih modela.
U svakom slučaju, demokratija zavisi od glasova građana. Na dan izbora hiljade ljudi dođe na birališta i glasaju, a njihovi listići se potom prebrojavaju da bi se saznalo ko je najpopularniji kandidat. Međutim, Arrow kaže kako u sistemu gdje ljudi biraju između više opcija ovo nije moguće postići a da se ne prekrši barem jedno od pet pravila koja bi trebalo poštovati.
Ta pravila su:
- Univerzalnost – Sistem bi trebao uvažiti svačije preference
- Odsustvo diktature – Niko ne može odrediti redoslijed tuđih preferencija
- Paretov princip – Ako je svakome draže A nego B, onda i grupi A mora biti draže nego B
- Nezavisnost nerelevantnih alternativa – Ako nakon izbora dodamo ili oduzmemo treću opciju, redoslijed prve dvije preference mora ostati nepromijenjen
- Prijelaznost – Ako grupa preferira A u odnosu na B, te B u odnosu na C, onda mora preferirati i A u odnosu na C.
Međutim, matematika kaže kako nije moguće kreirati izborni proces u kojem će se zadovoljiti svih pet kriterija koji bi garantirali da će kolektiv prilikom izbora između nekoliko opcija izabrati onu koju svi preferiraju!
Pogledajmo primjer sa gaziranim sokom, limunadom i običnom vodom kad su u odlučivanje uključene tri osobe od kojih svaka ima svoju listu preferencija od najdražeg do najmanje dragog.
Osoba A: Sok > Limunada > Voda
Osoba B: Limunada > Voda > Sok
Osoba C: Voda > Sok > Limunada
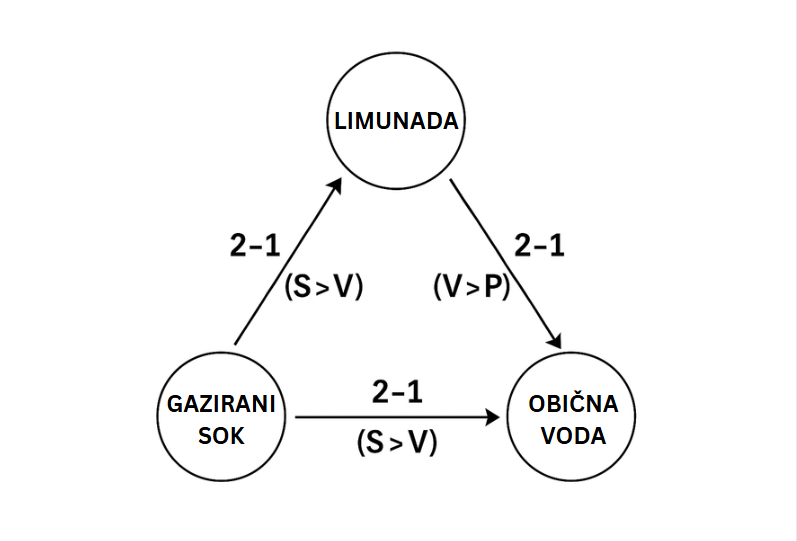
Koje će piće grupa naručiti na osnovu većinskog glasanja po parovima? Krenimo korak po korak, par po par…
- Sok vs Limunada
- A bira: Sok
- B bira: Limunada
- C bira: Sok
Sok pobjeđuje (2:1)
- Limunada vs Voda
- A bira: Limunada
- B bira: Limunada
- C bira: Voda
Limunada pobjeđuje (2:1)
- Voda vs Sok
- A bira: Sok
- B bira: Voda
- C bira: Voda
Voda pobjeđuje (2:1)
Dakle, ako sok pobjeđuje limunadu (1), i limunada pobjeđuje vodu (2), prema načelu prijelaznosti bi sok morao pobijediti vodu. Međutim, to se ne dešava i grupa će prema (3) piti vodu.
Upravo ovo je zaključak Arrowljevog paradoksa, koji sugeriše da se ovakve stvari dešavaju u bilo kojem sistemu gdje glasa više ljudi, gdje su ponuđene više od dvije opcije i gdje se pokušavaju zadržati fer pravila (nema diktatora, svi imaju jednak glas itd.).
Jednostavno rečeno, ne postoji sistem glasanja u kojem ne postoji diktator, a koji će stvarno odraziti preference pojedinaca i dati logičan i konzistentan rezultat kad su na raspolaganju više od dvije mogućnosti izbora. Čak i kad svi pojedinci glasaju savršeno racionalno i konzistentno, kolektiv u cjelini može završiti sa iracionalnim odabirom i nijedan sistem ne može zagarantirati razuman zbir pojedinačnih odabira.
Iako ovo može zvučati kao argument protiv demokratije, to nije ni izbliza tačno. Teorema nemogućnosti koju je postavio Kenneth Arrow ustvari samo ukazuje na ograničenja koja sa sobom nose demokratija i kolektivno donošenje odluka. To što bi zbir glasova na kraju mogao biti nerazuman ipak ne oslobađa birače obaveze da glasaju razumno. Štaviše, čak nas na to i obavezuje.


